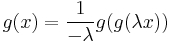Feigenbaum function

In the study of dynamical systems the term Feigenbaum function has been used to describe two different functions introduced by the physicist Mitchell Feigenbaum:

• the solution to the Feigenbaum-Cvitanović functional equation; and
• the scaling function that described the covers of the attractor of the logistic map

Functional equation

The functional equation arises in the study of one-dimensional maps that, as a function of a parameter, go through a period-doubling cascade. The functional equation is the mathematical expression of the universality of period doubling. The equation is used to specify a function g and a parameter λ by the relation

with the boundary conditions

• g(0) = 1,
• g′(0) = 0, and
• g′′(0) < 0

For a particular form of solution with a quadratic dependence of the solution near x=0, the inverse 1/λ=2.5029... is one of the Feigenbaum constants.

Scaling function

The Feigenbaum scaling function provides a complete description of the attractor of the logistic map at the end of the period-doubling cascade. The attractor is a Cantor set set, and just as the middle-third Cantor set, it can be covered by a finite set of segments, all bigger than a minimal size d_n. For a fixed d_n the set of segments forms a cover Δ_n of the attractor. The ratio of segments from two consecutive covers, Δ_n and Δ_n+1 can be arranged to approximate a function σ, the Feigenbaum scaling function.

See also

• Logistic map
• Presentation function

References

• Weisstein, Eric W., "Feigenbaum Function" from MathWorld.
• Feigenbaum, M. (1978). "Quanitative universality for a class of nonlinear transformations". Journal of Statistical Physics 19 (1): 25–52. Bibcode 1978JSP....19...25F. doi:10.1007/BF01020332. MR0501179. 
• Feigenbaum, M. (1979). "The universal metric properties of non-linear transformations". Journal of Statistical Physics 21 (6): 669–706. Bibcode 1979JSP....21..669F. doi:10.1007/BF01107909. MR0555919. 
• Feigenbaum, Mitchell J. (1980). "The transition to aperiodic behavior in turbulent systems". Communications in Mathematical Physics 77 (1): 65–86. Bibcode 1980CMaPh..77...65F. doi:10.1007/BF01205039. 
• Epstein, H.; Lascoux, J. (1981). "Analyticity properties of the Feigenbaum Function". Commun. Math. Phys. 81 (3): 437–453. Bibcode 1981CMaPh..81..437E. doi:10.1007/BF01209078. 
• Feigenbaum, Mitchell J. (1983). "Universal Behavior in Nonlinear Systems". Physica 7D: 16–39. Bibcode 1983PhyD....7...16F. doi:10.1016/0167-2789(83)90112-4.  Bound as Order in Chaos, Proceedings of the International Conference on Order and Chaos held at the Center for Nonlinear Studies, Los Alamos, New Mexico 87545,USA 24-28 May 1982, Eds. David Campbell, Harvey Rose; North-Holland Amsterdam ISBN 0-444-86727-9.
• Lanford III, Oscar E. (1982). "A computer-assisted proof of the Feigenbaum conjectures". Bull. Am. Math. Soc. 6 (3): 427–434. doi:10.1090/S0273-0979-1982-15008-X. MR0648529. 
• Campanino, M.; Epstein, H.; Ruelle, D. (1982). "On Feigenbaums functional equation 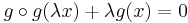". Topology 21 (2): 125–129. doi:10.1016/0040-9383(82)90001-5. MR0641996. 
• Lanford III, Oscar E. (1984). "A shorter proof of the existence of the Feigenbaum fixed point". Commun. Math. Phys. 96 (4): 521–538. Bibcode 1984CMaPh..96..521L. doi:10.1007/BF01212533. 
• Epstein, H. (1986). "New proofs of the existence of the Feigenbaum functions". Commun. Math. Phys. 106 (3): 395–426. Bibcode 1986CMaPh.106..395E. doi:10.1007/BF01207254. 
• Eckmann, Jean-Pierre; Wittwer, Peter (1987). "A complete proof of the Feigenbaum Conjectures". J. Stat. Phys. 46 (3/4): 455. Bibcode 1987JSP....46..455E. doi:10.1007/BF01013368. MR0883539. 
• Stephenson, John; Wang, Yong (1991). "Relationships between the solutions of Feigenbaum's equation". Appl. Math. Lett. 4 (3): 37–39. doi:10.1016/0893-9659(91)90031-P. MR1101871. 
• Stephenson, John; Wang, Yong (1991). "Relationships between eigenfunctions associated with solutions of Feigenbaum's equation". Appl. Math. Lett. 4 (3): 53–56;. doi:10.1016/0893-9659(91)90035-T. MR1101875. 
• Briggs, Keith (1991). "A precise calculation of the Feigenbaum constants". Math. Comp. 57 (195): 435–439. Bibcode 1991MaCom..57..435B. doi:10.1090/S0025-5718-1991-1079009-6. MR1079009. 
• Tsygvintsev, Alexei V.; Mestel, Ben D.; Obaldestin, Andrew H. (2002). "Continued fractions and solutions of the Feigenbaum-Cvitanović equation". C. R. Acad. Sci. Paris, Ser. I 334 (8): 683–688. doi:10.1016/S1631-073X(02)02330-0}. 
• Mathar, Richard J. (2010). "Chebyshev series representation of Feigenbaum's period-doubling function". arXiv:1008.4608 [math.DS]. 
• Varin, V. P. (2011). "Spectral properties of the period-doubling operator". KIAM Preprint 9. http://www.keldysh.ru/preprint.asp?id=2011-9&lg=e.